Why Is Science "Boring"?
OK, so, now that I don't spend my days teaching anymore, my friends and family are amazed at the fact that I can't stop learning new things, starting new projects, getting up at 6am and carrying on carrying on.
The worst part? I've kept the habit of a teacher and try to enthuse people about the stuff I discover / learn about... To mixed success.
This has led me to thinking about a worrying trend I find in online and offline conversations that may or may not be linked to conspiracy theories and "fringe" opinions.
The urge to publish was definitely tickled by this toot
Folks who don't understand AI like it more but once they understand it they find it less appealing
Where are you coming from?
First off, it's quite a big topic, one that can probably fill a few PhD thesises (thesii?) for a sociology/psychology department. This are just my thoughts about it, based on anecdotal evidence and cursory research. Feel free to hit me up about it, I'm totally open (and maybe even hoping) to be proven wrong.
As someone trained in linguistics, I feel the need to make sure the terms I'm using are somewhat well defined:
- "Science" as in the process of learning or discovery (in a greek sense closer to Μάθημα - Máthēma, something like the act of learning) is kind of alive and kicking, albeit in a weird way
- "Science" as in the established knowledge (in a greek sense closer to Γνόσι - Gnósī, whether collectively or privately) is very much in a state of active battle, and probably the one I have the most thoughts about
I'm sure some people will be thinking I'm preaching to the choir here, but I've seen with my own eyes the decline of visibility (in a positive sense) for the experts. Let me paint the scene for you:
We are in a meeting with half a dozen experts of their field and a couple of manager/investor types. The experts are disagreeing on many things but not on the most fundamental one: the proposal will not work. After the meeting, they are branded as killjoys, a vague social post arguing that the proposal is a good idea is brandished, and the decision to move forward is taken, to predictable results.
I'm not saying it's always the case, mind you. But more often than not, I have sat in auditoriums, meetings, what have you, and looked at a group of non-experts slowly but surely convincing themselves that the people they invited to talk (and sometimes even paid to do so) were wrong.
For someone who grew up in a time when science communicators were mostly researchers talking about their active research on live television, this is quite a culture shock. That's why I thoroughly enjoy youtube channels like Computerphile, who show actual research scientist being passionate, whether or not they are what is considered to be "good communicators" (and they are quite decent communicators, too!)
But the fact is, we have clearly entered an era where science communicators are permanent fixture. And I'm not throwing shade at them at all! They do a great and needed job.
But, when you ask them, one of the very first thing most of them will say is that they aren't "real" scientists (I beg to differ), and that they are like a gateway drug: get people interested in the topic so that they will dig deeper in the "actual" science.
What it feels like is that this worthy goal is never achieved.
The 10-minutes version of what could fill hours of lectures is enough: Γνόσι has been achieved, and Μάθημα is satisfied.
The problem is that it cuts both ways: a skilled communicator promoting pseudoscience will get the apparent same result as the one talking about what actual science says.
Milo Rossi (aka Miniminuteman on YouTube) has a fascinating lecture on his own field, right there on his channel
His central thesis seems to be that because communicating instantly to millions of people has become cheap, easy, and to some extent make enough money and/or fame back to the creator to encourage them to "challenge" the status quo, and find their audiences.
And, just like him, I find our position delicate: how do we promote the experts' words while not gatekeeping - preventing genuinely curious people to go and do their own research and experiments in good faith (as opposed to the derided "do your own research" mantra used by conspiracy theorists everywhere)?
Fine, but are you an expert in expertise?
Oof, good point, well made.
Here are my bona fides, and my experience on the matter. I will let you decide if it invalidates everything I have to say about it not.
I have been teaching classes in maths, computer science, data, and (machine) learning, as well as training other people in giving classes in front of audiences, for a couple of decades. There are definitely areas where I do decent, and others where I totally suck. You'll have to ask my students if I was overall a good teacher or not.
But objectively, a large majority of the people I trained went on to have a career in the field that I was in charge of teaching them, so I think it went decent. And while there were many, many, many, complaints, these are students we're talking about, and the power dynamic at play - me grading them based on "arbitrary" goals - means a somewhat antagonistic relationship, even when friendly. The grading game is a very heavy bias in your appreciation of teachers. I know. I even tested it: classes without an evaluation at the end tended to be lauded wayyyyyyyyy more than "strict" and friendly teachers.
Before we carry on with the central thesis of this post that will probably end up being way too long, here's a couple of observations I made as the head teacher / managing teacher of the curriculum:
- I had the chance of heading a department where the jobs the students would get at the end paid very well. (Too well? Yes probably, especially given the fact we still refuse to be an industry)
- Students attending class had a variety of incentives to specialize in CompSci, but let's not kid ourselves: making money was part of the equation.
- The highest paying jobs are usually the ones requiring the most expertise, or at least this used to be the case.
- So therefore, students should be trying to acquire as much expertise as possible, as fast as possible, to land those high-paying (and/or fun, and/or motivating, ...) jobs
Right?
Except: Students had a tendency to "check out" fairly rapidly
- "Copypasta" has been a thing forever, but when your exam takes place on a machine literally designed to make the process of finding something on the web and copying it in your production easier (and now AI that automates - badly - most of it), the incentive to "waste" an hour on something that would "grade" the same in a minute is hard to find.
- And during class, because the slides are available, or it's recorded, or there's a good chance to find a 10 minute video on "the same topic" online, why not do something more fun, and catch up later?
- If the passing grade is 10/20, and having more isn't rewarded, why go the extra mile?
Subsequent conversations with them yielded interesting observations, on top of those fairly obvious ones. What they told me they yearned for was "engagement" or "entertainment". and it's a whole Thing. Make learning fun, they say!
While I do agree with the sentiment (learning is fun, to me), I find myself obligated to point out that in this particular instance, it doesn't have to be fun: they were ostensibly there to get a good paying job (among other things). I mean, I'm training people to compete with me for jobs and contracts, and I have to make them feel entertained?
Regardless of the validity of that demand, I always did strive to make the learning fun, because it's fun - to me. But I always found the reversal of expectations weird: here you are, asking me for a favor, and I have to thank you by entertaining you?
I totally understand how that may sound gatekeeper-y and demeaning. And, again, I never actually subscribed to that attitude, but when you think about it for a minute, there definitely is a difference between learning something that will be used to earn a living, and learning things without ulterior motives - at the beginning at least. Because of my well-ingrained biases regarding the former, I will keep the rest of this post to the latter: learning stuff that may not net an immediate advantage.
You're gonna talk about history now, aren't you?
Yes. Giving context and a bit of epistemology is part of the scientific method. Plus it's a fascinating topic in and of itself. It will happen.
I'm not going back too far though, only to the printing press, and the Renaissance (or Early Modern Era as I learned it should probably be called, because it was only a rebirth for Western Europe, not really the whole world where they didn't have our wonderfully repressive period known colloquially as the Dark Ages).
Scientists then, like now, had feuds about their hypothesises (hypothesi?), and wrote scathing articles, pamphlets, and letters, about their colleagues who were obviously wrong. Because of the wide dissemination of ideas and a general curiosity about how the world actually worked in a more practical way than "oh well, it's the will of a deity" or "well, my grandparents did it that way so it must carry on the same", there was a crowd - yes an actual crowd - coming to hear the latest discoveries at the various academies.
It's kind of like a Youtube channel, but you had to go to an auditorium once a month or whatever, to hear, usually from the mouth of the actual scientist or one of his proxies (student, secretary of the academy, colleague) what the exciting new scientific discovery was. And if you couldn't make it, there were local clubs and academies that would debate the written reports of the lecture.
Scientists were household names, and pride of their countries. You have a Gauss? Well we have a Newton! A lot of streets, buildings, and areas, are still named after them, and you were expected to be able to quote them before entering a debating arena.
And yet, there were close to no intermediary to the content of their theories: the people read the articles or letters verbatim. Science communication was without added value. If you wanted to participate in those discussions, you had to learn the whole thing, not just the cliff notes version.
The weird part is that while this feels super elitist - you have to be a world class mathematician to contribute to a discussion of the latest math discovery - it was fairly open. As long as you had enough free time (that is elitist, for different reasons) to learn, and could back your claims up in front of renowned scientists with the proper methodology, you were part of the club. A lot of scientists up until the Industrial Revolution were not just scientists. Enormous scientific discoveries and contributions were made by people with practical knowledge that wanted to find out the why, or people with a lot of free time just engaging in science out of curiosity.
That popular interest in discoveries and science continued unabated up until very recently. Scientific magazines, and, as I said before, scientists on TV, were very popular, up until the complete takeover of the Internet as a source of knowledge.
For reference, here are the circulation numbers for the scientific magazines here in France (may I suggest diving into those stats? Apart from being paper scans and sometimes hard to decipher, there aren't any regular format or nomenclature. Makes for a fun afternoon of research!):
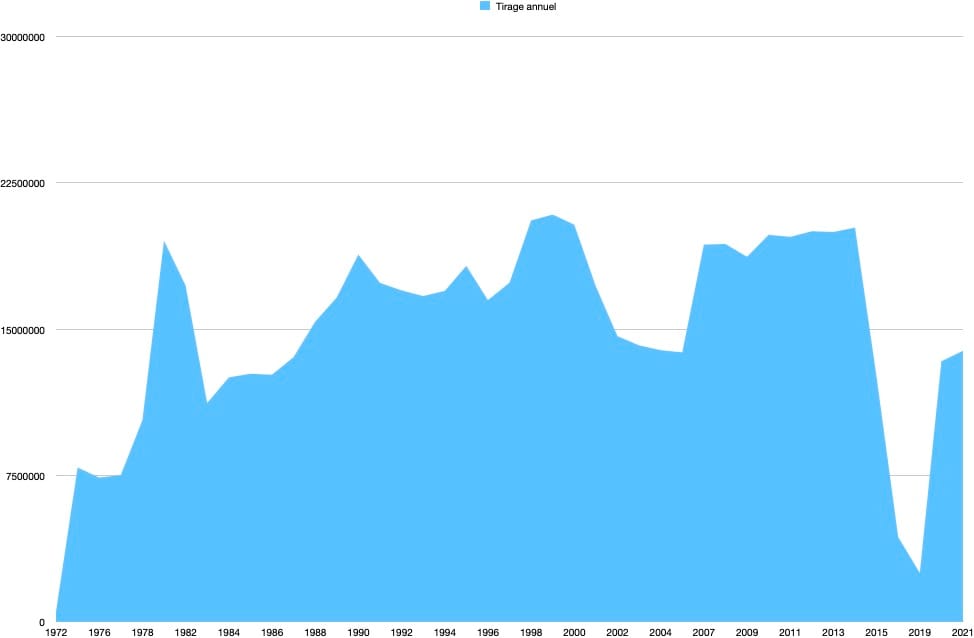
What's surprising to me is the resurgence super recently. But you can clearly see the peak in 1981 among a global rise in interest about science & tech magazines, then the peak / dip around the Y2K bug, and since 2014-ish a sharp decline.
Obviously, this is only the number for France, and if you take a peek at the data itself, you'll see that there is a margin for error (what exactly is included in that category is arbitrary to a point). But it matches my gut feeling, so there is that.
Of course, nowadays, the undisputed royalty of scientific communication is the Internet. Science communicators have setup many very interesting channels, as I mentioned before, and most of the good ones are quite humble despite the fact that they have a viewership that the equivalent press would have considered a dream only a couple of decades ago.
Scientific honesty starts with, and carries on with, "I may be wrong" - always. Even when your theory (in the scientific sense, not in the vernacular "hypothesis" sense) seems to tick all the boxes and match all the data, there is a small chance that it could be at worse wrong except in this particular case, and at best right but only as as part of a more general theory. Again, watch people like Milo Rossi to see how they deconstruct their own certainties and doubts publicly.
So, with that historical context in place, let's talk about the iceberg.
The iceberg as in the thing that sunk the "insubmersible" Titanic?
More as in the thing that is mostly underwater. Because we have an Iceberg Problem.
The openness of science is still a thing most scientists strive for, but in order to understand - or even contribute - to modern research, you can't really do it in your free time and as a dilettante anymore, however brilliant.
Let me give you a personal example: I tried to teach a class on native mobile development. Despite what most platform vendors (and now IA vendors) would have you believe, software development isn't easy. Sure, if you have an image of something you want to put on the web (a landing page, a presentation page, anything that you could compose in a word processor or a page layout piece of software), making "a web site" that matches the visuals is fairly simple.
And, if you're only interested in what everybody else is doing, there's a good chance that someone out there does it already and could either sell it to you or give it for free.
This blog is easy to "make": I open a web browser, and type something in the window and blammo, you can read it. Except... this is only the tip of the iceberg.
Your web browser has more than 20 millions of lines of code, it runs on an operating system that is a couple of orders of magnitude more complex than that. And on my end, the server also has millions of lines of code. All of that requires maintenance by someone you don't know, and, more likely than not, that you haven't paid.
That's something of a marvel to me that despite the poor design choices we inherited, and the average number of bugs per 10k lines of code, when you write <center>something</center>, it is somewhat in the middle of the page. If it's not, then you're in for a whoooooooooooole lot of debugging time.
Back to my native development class: it's "lower level" than the web, which, in practice, means that there is one or two less layers of millions of lines of code for my "hello world" to be displayed somewhat properly. Oh and you add some real life issues such as battery and network performance into the mix, which you don't really have to care about "on the web".
What it meant is that my first class struggled with concepts and underpinnings that they never had to think about before. So I had to add more hours to the class. Then to add some pre-requisites in the years before. Then a whole new kind of course around designing and debugging code.
Because, you see, there's a whole lot of things under the hood that work just fine for 80% of what you want to do. The rest is trying to figure out why it doesn't and decide whether it requires a workaround of some weirdness in the underlying structure, or a completely new thing that has to be built from scratch.
In practice, what it means is that you can cobble something that looks like it's working fine enough without much training, but as your work is exposed to more users and situations, the probability of it breaking goes up exponentially. And you may not have any idea why.
Anyways, enough of my own field, it holds mostly true for every single one nowadays: in order to understand the current physics, the level of maths and prior work needed to "get it" is astounding. And it's an immediate turn off for a lot of folks.
Plus, because a lot of the most graspable concepts have been known and integrated into our lives for so long, the incentive to understand the current forefront of a scientific field boils sometimes down to "do I have time?" which correlates neatly to "what purpose does it serve?" and "how does it benefit me?"
If you knew the most current theories of physics, say 300 years ago, it might give you an edge in your daily life, like using levers instead of wrecking your back. Then it was about how does it help me "professionally"? Like using pulleys in your factory instead of 20 sweaty dudes. Nowadays? Practical applications of physics research may help someday a mega corporation that will sell me something that makes my life a lot easier.
So, it's all about curiosity, except when it's your job to be at the edge of what can be done.
But people still consume a lot of "educational" content, are they not?
Time for a tangent. Curiosity has always felt like a two-headed thing to me. There's "genuine" curiosity - as in "how is it possible? I'd like to know more about how or why this thing is" - which is almost always the starting point of research both personal and institutional, and there's ἐκρυπτός (ekrīptós), hermeticism, esotericism, arcanism, which are more about what I know that you don't, and is about power.
Because, yes, knowledge is power, even when it's not science. Power over people, power over situations, power over the machine,... If you know stuff, you're less passive, less at the mercy of whatever or whoever is guiding the situation you are in. And it's quite intoxicating to feel in control, or at least "understand the plan" for most people.
Just look at the success of gossip, magic tricks and the like! And in my field it's especially prevalent. If a company/freelancer doesn't tell the potential customer that it would probably cost a lot less to do their thing using a very well maintained and fairly easy to learn piece of free software, they may be able to extract quite a lot of monies from them.
That's why I'm particularly careful with science vulgarization in particular, and "knowledge" communication in general. Again, many people have written books and made videos and all that about it, but the incentives of the person giving you information factor in how I parse said information.
Now, the issue is, it's exactly what pseudoscience aficionados say as well. "The establishment (whatever that is) is lying to you, seek your own truth."
Let's talk incentives then shall we?
On the one hand, you have governmental and/or scientific cabals, that invest billions of monies into maintaining a fiction about some lie being the truth that involves thousands or millions of people that have to be bribed, coerced, intimidated, and what have you, in order to keep the "population" (ie you, and me) in a state of... compliance? Tranquility?
On the other hand, you have that person on the internet that knows the truth that is hidden and benefits financially and in terms of fame from your viewership.
Oh and those all powerful governments who managed to keep a lid on things for so long and at great expense somehow fail to take down the videos of Joe Schmock from Nowherville.
While doubting governments (because, yes, they do lie, hide and/or mismanage the truth sometimes) is totally fair in many many areas, science isn't "governmental". A random research team in Brazil do their thing, formulate hypotheseseseesses (hypothesi?), include them in a theory, and publish it for another set of random teams in Japan and Kenya to conform or deny.
You're telling me that the French government, which is publicly fighting with many governments over a lot of issues (and has warred because of it, too) is somehow coordinating with the UK to hide the truth about the moon landings while accusing them of lying about almost everything else?
Sorry about the choice of examples, but it's currently the 6 Nations tournament, and we French and English love to hate each other during tournaments. Especially Rugby. So, there. Apologies all around.
How does that relate to science being "too boring"?
Glad you asked. So, in my mind, the appetite for "trivia" or for useful knowledge (the kind that gives you a job, or power, or fame, or monies) hasn't abated at all. But actual modern science requires effort and dedication to understand.
Going back to my own field, if I can earn $10k with a customer who wants a website by doing $30 worth of work, why wouldn't I? (I mean except for honesty, ethics, love of humanity, long term reputation effects, risk of being found out as a fraud and a swindler, and many many more reasons)
And if I can tell that customer that they will never have the time to learn all the esoteric knowledge that justifies that price tag and they can't have a decent picture of the truth in my words, I win, right? (Power, again)
The reality is, most of my knowledge is boring tedium (for most people) about bits and bytes, algorithms that were thought of and perfected over a long period of time, a lot of "yea we do this like that because it's what we've always done, so all the tools are geared that way, like it or not", a dash of general understanding of maths and physics, and lots and lots and lots and lots of lessons learned from past mistakes.
In order to know as much as me, you don't have to be particularly smart. You have to put in the hours and do the mistakes. Experience is a catalog of dead ends that I know to avoid and you don't. It's as simple as that, mostly.
And most of science is that way: it's a pyramid that is now so high that no one has the time to learn from top to bottom, except for people whose job it is. But there is power to be gained from the tip. Funding for researchers, fame for communicants (and monies too), glory for nations, and, yes, all of the above for fakers and frauds too.
Once you start establishing your bona fides by explaining the layers your current expertise relies on, you are "boring" compared to your competition - the people who may not know as much as you, but are far more entertaining in their presentation - who just doesn't care about being right, just about being right enough.
And so we have pseudoscience that promises "secret knowledge" and power over your "sheeple" condition.
And we have noise about competing theories or discoveries for research grants.
And we have hiring issues.
In all my years training people, it's a sad observation to realize that it's not necessarily the most knowledgeable who get the high-paying job. I've met and trained genuinely curious, smart and motivated people who struggled to get hired. I've met single minded researchers that were working on something that could benefit humanity as a whole get their research grant denied, or so heavily hogtied with strings attached that it made the act of searching meaningless. It's not necessarily true for all the smart and/or knowledgeable people I've met, but the percentage is high enough to make me sad.
The scientific method works so well because it's predictable, open, and slow. As opposed to surprising, arcane, and fast. And therefore, yes, it's boring.
But it's boring in the same way that doing the scales and noodling on your instrument for hours before you take the stage is boring. It's boring in the same way the characters in your novel / movie / tv show slowly work towards winning at the end.
It's boring if you consider only the process and the ongoing effects, rather than the potential for apotheosis.
You said "AI" earlier. That was just clickbait, right?
Point of origin, rather than clickbait. And one I will address now.
Back in the Before Times, I was asked to moderate a panel on the use of AI in finance. You can still see the video here.
These people have invested a lot of time, money and expertise, into trying to make products using AI, with customers who are very picky and take big risks when using their expertise in the field.
AI as it understood these days (LLMs, agents, domain-specific models,...) works of a pyramid of technologies and assumptions, some more hidden than others. What do I mean by that?
Without delving too deep in the technical side, the pipeline is as follows:
- Gather a lot of data (assumption: this data is relevant to the rules, that data isn't)
- From this data try to infer correlations and "rules" (assumption: there is a rule albeit an arcane one)
- Compile these rules into a model (assumption: the modelling will capture the rules)
- "Apply" the model to new data, and witness that if you follow those rules, the output should be X (assumption: new data will fit in the ruleset of the model)
For Large Language Models, the data is text. The system tries to infer words (or sequences of words) based on whatever words were given as input. If you build your model on questions and answers, what you get is something that will try to guess the probability on a sequence of words being the correct answer to another sequence of words that are considered to be a question.
That model will not be able to handle anything that is not a question, or that is a question but on a topic is has never seen before. Technically it's impossible.
And herein lies my problem with the current marketing of AI as a panacea: because most people do not understand the pipeline underneath, they cannot interpret the output properly: the model will always give you an answer, but with probabilities attached.
In my example, if I give my question/answer model the input "my dog barks at birds and the sky is blue", it might output something along the lines of "the sky is blue because of refraction in the atmosphere that scatters the red light" but with a probability (aka confidence) of 0.4.
If you've ever seen a matching algorithm (recommendation for buying stuff, dating sites, whatever), the underlying principle is the same... it tries to match an output with your input.
Now if you use the user-friendly version of whatever LLM you want, it won't give you that. It will output with absolute authority the answer that best matches your input, based on whatever data it was trained on. You usually do not get the nitty gritty probability numbers, and therefore how "confident" the model is it performed correctly.
On top of that, the companies that sell you access to their LLMs also have algorithms and rules that will parse the model's output and modify it, while hiding the inner workings, unless you write code to tap into the lower level - their APIs.
Their incentive is to look authoritative so that the product itself doesn't appear wonky (can you imagine a car salesman that would tell you the car may work fine a lot of times but they don't know if it will work on your driveway?) by hiding all the genuinely cool stuff underneath, and make it appear as magical and useful as possible.
BUT in order to have a somewhat reliable model, it has to be Large, because the moment the model encounters something completely outside of what it knows the probabilities of, it will output nonsense. And that precludes most of the personal experimentations that curious people may have.
The systems, principles and techniques are simple. Data in, a bit of probabilistic maths, and data (with attached probability) out. Having access to enough training data, and the computing power to find out the relationship between every possible input and every possible output is staggeringly difficult.
So you can't really check if the model was properly trained (or train it yourself), or even if the output has a high confidence, because the one thing that models can't do is say "I don't know". They will tell you instead gibberish, with a low confidence rating, which is their way of saying that they can't fulfill your desires. And that part is hidden for a large majority of the users.
And so we're back to asserting stuff with confidence, and the difficulty of distinguishing an actual expert from someone who can say stuff nice.
Not clickbait, alright?
I don't get it. Is science boring?
I don't think so. It requires a bit more effort nowadays than witnessing parlor tricks or being told in 10 minutes about a thing. But it also ranges quite far. We do things daily that were unthinkable a couple of generations ago.It's just that, because the effect is mundane, it's lost a bit of appeal. But it's still so fascinating and so cool, if you look at how such a mundane thing is done. Just last year in 2024, we accomplished things as a species that are completely and totally amazing, if you stop and think about it:
We're hopefully, finally, on the cusp of preventing HIV. A disease that infects more than a million people every year and kills two thirds of that. Every. Single. Year. And we are making progress in understanding the virus and fighting it. The cure isn't here yet, but we're getting better at preventing and fighting it.
Japan managed to soft land (ie not crash) a human sized object on the moon with a precision of a 100 meters, after a trip of 400 000 kms! That's like putting the billiard ball in the pocket from 440 km away. How's that not amazing?
Speaking of space, our species launched a spacecraft the size of car on a journey that will take 6 years, just to take a better look at a bunch of moons in orbit around Jupiter. We can do that.
We also found the oldest settlement to date in the Amazon rainforest, and we didn't even have to remove the trees to do so. Like, these cities were built and abandoned millenia ago, they are immensely difficult to access, and there was a decent chance it was just a fluke of nature to see patterns in the jungle, but with LIDAR and lots of careful analysis, those ruins are within the realm of human knowledge once again.
And I'm sure that in a field that you take an interest in, there were many advances and discoveries.
I may submit to the unknown, but never to the unknowable
- Yama, Lord of Light, Roger Zelazny - 1967
